 
***********************************************************************
Fibonacci Sayıları ve Altın Oran:
İtalyan matematikçi Fibonacci yazdığı matematik kitaplarından birinde tavşan çiftliği olan bir arkadaşıyla ilgili olduğunu iddia ettiği bir problem sorar.Bu probleme göre çiftlikteki tavşanlar doğdukları ilk iki ay yavru yapmazlar.Üçüncü aydan itibaren her çift her ay bir çift yavru yapar. İlk ay yeni doğmuş bir çift tavşan vardır.İkinci ayda bu tavşanlar henüz yavrulamadıkları için hala bir çift tavşan vardır.Üçüncü ay bunlar bir çift yavru verir ve iki tavşan olur.Yeni doğan çift dördüncü ay doğurmayacak,oysa ana babaları yeniden bir çift yavru yapar ve toplam üç çift tavşan olur.Bu şekilde devam edilirse; tavşan çiftleri aylara göre şu sıralamayı ortaya koymaktadır: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,... Görüldüğü gibi ilk iki sayı hariç, her sayı kendisinden önce gelen iki sayının toplamına eşittir.
Altın oran, 1 sayısına eklendiğinde kendi karesine eşit olan iki sayıdan biridir. Altın oran 1,618033.... olarak devam eden ondalık sayıdır. 1 sayısına eklendiğinde kendi karesine eşit olan diğer sayı da - 0,618033... olarak devam eden ondalık sayıdır.
Sanatçılar bu özelliği kullanıp göze güzel görünen eserler meydana getirmişlerdir. Örneğin Mona Lisa tablosunun boyunun enine oranı altın oranı verir. Mona Lisa'nın yüzünün etrafına bir dikdörtgen çizdiğinizde ortaya çıkan dörtkenar bir altın dikdörtgendir. Bu dikdörtgeni, göz hizasında çizeceğiniz bir çizgiyle ikiye ayırdığınızda yine bir altın oran elde edersiniz. Resmin boyutları da altın oran oluşturmaktadır.
Bir çok bitki filizlendiğinde, önce bir adet yaprak verir. Bir süre sonra bir yaprak daha açar, sonra iki tane daha... Sonra üç, beş, sekiz, onüç, yirmibir, otuzdört, vs. Pek çok bitki büyüme prensibi olarak kendisine Fibonacci ardışığını seçmiştir.
MATEMATİĞİN SİHİRLİ SAYISI
ALTIN ORAN:doğada sayısız canlının ve cansızın şeklinde ve yapısında bulunan özel bir orandır.Altın oran, doğada, bir bütünün parçaları arasında gözlemlenen, yüzyıllarca sanat ve mimaride uygulanmış,uyum açısından en yetkin boyutları verdiği sanılan geometrik ve sayısal bir oran bağıntısıdır. Doğada en belirgin örneklerine insan vücudunda, deniz kabuklulularında ve ağaç dallarında rastlanır.Platon'a göre kozmik fiziğin anahtarı bu orandır. Altın oranı bir dikdörtgenin boyunun enine olan "en estetik" oranı olarak tanımlayanlar da vardır.
Eski Mısırlılar ve Yunanlılar tarafından keşfedilmiş, mimaride ve sanatta kullanılmıştır. Göze çok hoş gelen bir orandır.

Altın Oran:
CB / AC = AB / CB =Φ=1.618
Bir doğru parçasının (AB) Altın Oran'a uygun biçimde iki parçaya bölünmesi gerektiğinde, bu doğru öyle bir noktadan (C) bölünmelidir ki; küçük parçanın (AC) büyük parçaya (CB) oranı, büyük parçanın (CB) bütün doğruya (AB)oranına eşit olsun.
Altın Oran, pi (π) gibi irrasyonel bir sayıdır ve ondalık sistemde yazılışı; 1.618033988749894... dür. (noktadan sonraki ilk 15 basamak). Bu oranın kısaca gösterimi:
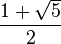 olur. Altın Oranın ifade edilmesi için kullanılan sembol, PHI yani Φ 'dir. olur. Altın Oranın ifade edilmesi için kullanılan sembol, PHI yani Φ 'dir.
İNSAN VÜCUDUNDAKİ ALTIN ORANLAR:
*ÇENE BAŞ UCU UZAKLIĞI:KULAKLAR ARASI UZAKLIK
*DUDAK KAŞ ARASI UZAKLIĞI:BURUN UZUNLUĞU
*DUDAK UZUNLUĞU:BURUN GENİŞLİĞİ
*YÜZÜN BOYU:ÇENE KAŞ ARASI UZAKLIĞI
*GÖZBEBEKLERİ ARASI UZAKLIK:KAŞLAR ARASI UZAKLIK
*İNSAN BOYU:AYAKLA GÖBEK ARASI UZAKLIĞI
*PARMAUCU DİRSEK ARASI:BİLEK DİRSEK ARASI
*OMUZ BAŞ UCU ARASI:ÇENE BAŞUCU
*GÖBEK BAŞ UCU:OMUZ BAŞ UCU
*GÖBEK DİZ ARASI:DİZ AYAK ARASI
*PARMAK BOYU:İLK İKİ BOĞUM UZUNLUĞU
*AKCİĞERDE UZUN BRONŞ:KISA BRONŞ
*DNA SARMALININ BİR YUVARLAĞININ UZUNLUĞU:GENİŞLİĞİ
BİTKİLERDE ALTIN ORAN:
Bir bitkiyi dikkatle incelerseniz fark edersiniz ki, yapraklar hiçbir yaprak alttakini kapatmayacak şekilde dizilmiştir. Bu da demektir ki, her bir yaprak güneş ışığını eşit bir şekilde paylaşıyor ve yağmur damlaları bitkinin her bir yaprağına değebiliyor.
Bir bitkinin sapındaki yapraklarında, bir ağacın dallarının üzerinde hemen her zaman BİR ALTIN ORAN SAYISI BULURSUNUZ..Eğer yapraklardan biri başlangıç noktası olarak alınırsa ve bundan başlayarak, aşağıya ya da yukarıya doğru, başlangıç noktasının tam üstünde veya altında bir yaprak buluncaya kadar yapraklar sayılırsa bulunan yaprak sayısı farklı bitkiler için değişik olacaktır ama her zaman bir ALTIN DİZİ ELDE EDİLECEKTİR.
BAZI ÖRNEKLER:
1. Ayçiçeği: Ayçiçeği nin merkezinden dışarıya doğru sağdan sola ve soldan sağa doğru tane sayılarının birbrine oranı, altın oranı verir.
2. Papatya Çiçeği: Papatya Çiçeğinde de ayçiçeğinde olduğu gibi bir altın oran mevcuttur.
|